Table of Contents
Introduction
In this series we introduce progressively the art of a new innovative, exhilarating, data modeling methodology that is based on R3DM conceptual framework. We want to engage software developers, architects, data model designers and everyone interested in learning the advantages of applying this method and the main differences from the data models of the past. We start with terms and constructs that most of us are familiar with from the relational database management systems and we dive into some detail of the Atomic Information Resource unit at Part 2. For coding purposes, we picked Wolfram Language, the 25+ years of development programming language of Mathematica. Wolfram Language combines symbolic, functional and rule-based programming with a vast library of built-in functions, a computational knowledge engine (Wolfram alpha) and a huge database of curated data.
Relational Constructs
The entity-relational data model (ERDM) is still the most popular data model in database management systems. You can think many reasons for this fact but from the user perspective the main reason is the simple and natural way of managing data in tables with rows (records) and columns (attributes). On top of that, SQL is a very powerful and easy to learn programming language that covers completely the relational operators on data sets. In this article various methods of representing the basic constructs of the relational model are demonstrated with Wolfram Language powerful transformations. You may download our Wolfram Notebook and try our examples in Wolfram Programming Lab or Wolfram Development Platform. The structured data for our example can be found at our Github repository
Product Type
In programming languages and type theory, a product of types is another, compounded, type in a structure. The “operands” of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed order, but otherwise may contain all possible instances of its primitive data types. The expression of an instance of a product type will be a tuple, and is called a “tuple type” of expression. A product of types is a direct product of two or more types - Wikipedia, Product type
Example: Integer x String x Colour
In Wolfram Language an instance of such a type is represented with the built-in List symbol:
In: partInstanceAsList = {991, "Left Handed Bacon Stretcher Cover", Red}
Out: 
And to check/verify the type for each element of the List we map the function Head
In: Head /@ partInstanceAsList
Out: {Integer, String, RGBColor}
Tuple (Record/Row)
A tuple is a finite ordered list of elements. In mathematics, an n-tuple is a sequence (or ordered list) of n elements, where n is a non-negative integer. In computer science, tuples are directly implemented as product types in most functional programming languages. More commonly, they are implemented as record types, where the components are labeled instead of being identified by position alone. This approach is also used in relational algebra.
In database theory, the relational model uses a tuple definition similar to tuples as functions, but each tuple element is identified by a distinct name, called an attribute, instead of a number; this leads to a more user-friendly and practical notation. A tuple in the relational model is formally defined as a finite function that maps attributes to values. In this notation, attribute-value pairs may appear in any order - Wikipedia, Tuple
In Wolfram Language record abstract data structure is usually represented with the Association function, i.e. a symbolically indexed list of Rules (key-value pairs).
In: partInstanceAsAssociation =
Association[
partID -> 991,
partName -> "Left Handed Bacon Stretcher Cover",
partColor -> Red ]
Out: <| partID->991,partName-> "Left Handed Bacon Stretcher Cover", partColor->Red |>
In: Values[partInstanceAsAssociation]
Out: {991, "Left Handed Bacon Stretcher Cover", Red}
In: partInstanceAsAssociation // Normal
Out: {partID->991, partName->"Left Handed Bacon Stretcher Cover", partColor->Red}
Attribute (Field/Column)
The basic relational building block is the domain or data type, usually abbreviated nowadays to type. A tuple is an ordered set of attribute values. An attribute is an ordered pair of attribute name and type name. An attribute value is a specific valid value for the type of the attribute. This can be either a scalar value or a more complex type. A domain describes the set of possible values for a given attribute, and can be considered a constraint on the value of the attribute. Mathematically, attaching a domain to an attribute means that any value for the attribute must be an element of the specified set. Constraints make it possible to further restrict the domain of an attribute - Wikipedia, Relational_model
In our example, two of our attributes partID is of integer data type and partName is of string data type. They both take scalar values. But the partColor attribute is of complex type and is defined in Wolfram Language with the function RGBColor.
In: Apply[Rule,
Thread[
{Keys[partInstanceAsAssociation], Head /@ partInstanceAsList}], {1}]
Out: {partID->Integer, partName->String, partColor->RGBColor}
Attribute can be seen as a mapping function. It maps a tuple to a value. We can define a function where we pass a single argument which is the association representation of the tuple and we return the specific value of the key. For example:
isIdentifierOf[assoc_]:=assoc[partID]
isNameOf[assoc_]:=assoc[partName]
isColorOf[assoc_]:=assoc[partColor]
{
isIdentifierOf[partInstanceAsAssociation],
isNameOf[partInstanceAsAssociation],
isColorOf[partInstanceAsAssociation] }
Out: {991, "Left Handed Bacon Stretcher Cover", Red}
Relation (Base relval)
In the relational model, a relation is a (possibly empty) finite set of tuples all having the same finite set of attributes.This set of attributes is more formally called the sort of the relation, or more casually referred to as the set of column names. A tuple is usually implemented as a row in a database table. The fundamental assumption of the relational model is that all data is represented as mathematical n-ary relations, an n-ary relation being a subset of the Cartesian product of n domains. In the mathematical model, reasoning about such data is done in two-valued predicate logic, meaning there are two possible evaluations for each proposition: either true or false (and in particular no third value such as unknown, or not applicable, either of which are often associated with the concept of NULL). Data are operated upon by means of a relational calculus or relational algebra, these being equivalent in expressive power.
A relation is defined as a set of n-tuples. In both mathematics and the relational database model, a set is an unordered collection of unique, non-duplicated items. A table is an accepted visual representation of a relation; a tuple is similar to the concept of a row. It is a set of tuples sharing the same attributes; a set of columns and rows. A relvar is a named variable of some specific relation type, to which at all times some relation of that type is assigned, though the relation may contain zero tuples - Wikipedia, Relation_(database)
- Predicates and the closed world assumption
A relation consists of a heading and a body. A heading is a set of attributes. A body (of an n-ary relation) is a set of n-tuples. The heading of the relation is also the heading of each of its tuples. The body of a relation is sometimes called its extension. This is because it is to be interpreted as a representation of the extension of some predicate, this being the set of true propositions that can be formed by replacing each free variable in that predicate by a name (a term that designates something). There is a one-to-one correspondence between the free variables of the predicate and the attribute names of the relation heading. Each tuple of the relation body provides attribute values to instantiate the predicate by substituting each of its free variables. The result is a proposition that is deemed, on account of the appearance of the tuple in the relation body, to be true. Contrariwise, every tuple whose heading conforms to that of the relation, but which does not appear in the body is deemed to be false. This assumption is known as the closed world assumption: it is often violated in practical databases, where the absence of a tuple might mean that the truth of the corresponding proposition is unknown - Wikipedia, Relation_(database)
In: SQLSelect[conn, "Parts", "ShowColumnHeadings"->True] // TableForm
Out: 
In: SQLSelect[conn, "Parts", "ShowColumnHeadings" -> True]
Out: {
{"pid", "pname", "pcolor"},
{991, "Left Handed Bacon Stretcher Cover", "Red"},
{992, "Smoke Shifter End", "Black"},
{993, "Acme Widget Washer", "Red"},
{994, "Acme Widget Washer", "Silver"},
{995, "I Brake for Crop Circles Sticker", "Translucent"},
{996, "Anti-Gravity Turbine Generator", "Cyan"},
{997, "Anti-Gravity Turbine Generator", "Magenta"},
{998, "Fire Hydrant Cap", "Red"},
{999, "7 Segment Display", "Green"}
}
View (Derived relvar / Result set)
In a relational database, all data are stored and accessed via relations. Relations that store data are called “base relations”, and in implementations are called “tables”. Other relations do not store data, but are computed by applying relational operations to other relations. These relations are sometimes called “derived relations”. In implementations these are called “views” or “queries” - Wikipedia, Relation_(database)
queryString = "
SELECT Catalog.catsid,
Suppliers.sname,
Catalog.catpid,
Parts.pname,
Parts.pcolor,
Catalog.catcost
FROM Suppliers
INNER JOIN (Parts
INNER JOIN [Catalog] ON Parts.pid = Catalog.[catpid]) ON Suppliers.sid = Catalog.[catsid]
WHERE (((Catalog.catpid)=998))
ORDER BY Catalog.catcost;
"
SQLExecute[conn, queryString, "ShowColumnHeadings"->True] // TableForm
Out:
Database
Each database is a collection of related tables; these are also called relations, hence the name “relational database”. Each table is a physical representation of an entity or object that is in a tabular format consisting of columns and rows - Wikipedia, Relation_(database)
In: SQLTableNames[conn]
Out: {"Catalog", "Parts", "Suppliers"}
In: SQLTableNames[conn, "TableType"->SQLTableTypeNames[conn]]
Out: {"MSysAccessObjects", "MSysAccessXML", "MSysACEs", "MSysIMEXColumns", "MSysIMEXSpecs", "MSysNameMap", "MSysNavPaneGroupCategories", "MSysNavPaneGroups", "MSysNavPaneGroupToObjects", \
"MSysNavPaneObjectIDs", "MSysObjects", "MSysQueries", "MSysRelationships", "Catalog", "Parts", "Suppliers", "View998Suppliers", "ViewAll"}
In: SQLTableInformation[conn, "ShowColumnHeadings"->True] // TableForm
Out:
Entity-Relationship (ER) Constructs
ER data model is a systematic way of describing and defining a business process. The process is modeled as components (entities) that are linked with each other by relationships that express the dependencies and requirements between them. Entities may have various properties (attributes) that characterize them. Diagrams created to represent these entities, attributes, and relationships graphically are called ER diagrams
- Enhanced Entity Relationship (EER)
The EER data model includes all of the concepts introduced by the ER model. Additionally it includes the concepts of a subclass and superclass (Is-a), along with the concepts of specialization and generalization. Furthermore, it introduces the concept of a union type or category, which is used to represent a collection of objects that is the union of objects of different entity types - Wikipedia, Entity–relationship_model
Record Representations
1. List
You need to maintain two ordered lists, one for the data values and another one for the semantics, i.e. the attribute/column names.
In: partInstanceAsList
Out: {991, "Left Handed Bacon Stretcher Cover", Red}
In: attributes={"pid","pname","pcolor"}
Out: {pid, pname, pcolor}
You can combine the two lists in one list of Rules with the following command
In: Thread[Rule[attributes, partInstanceAsList]]
Out: {"pid"->991, "pname"->"Left Handed Bacon Stretcher Cover", "pcolor"->Red}
A Rule is the equivalent of a key-value pair, but it is more powerful because in Wolfram Language it is the basic mechanism that is used in transformations. Nevertheless for lookup operations and updating Wolfram researchers added a more powerful construct that is called Association, see below.
2. Triples
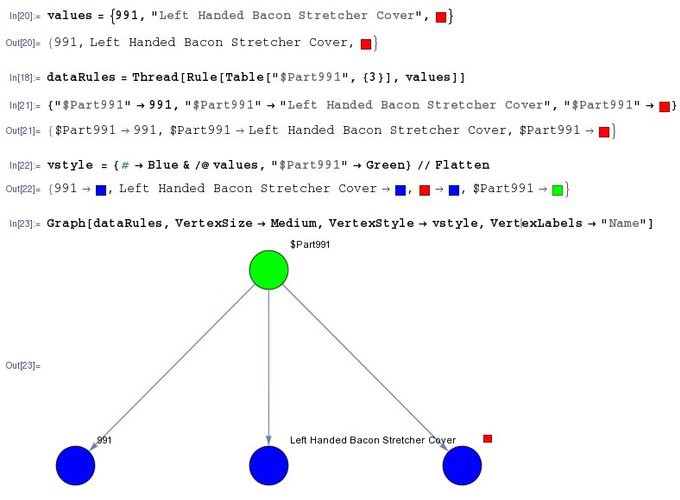
Let us call a specific part instance partXYZ, if we represent this as the subject resource of a triplet, the list of attributes as the predicates and the list of values as the objects we can take the following triplets
subject = Table["http://example.org/resource/partXYZ", {3}];
predicate = StringJoin["http://example.org/attribute/", #] & /@ attributes;
object = partInstanceAsList;
Transpose[{subject, predicate, object}] // TableForm
Out: 
3. Directed Graph
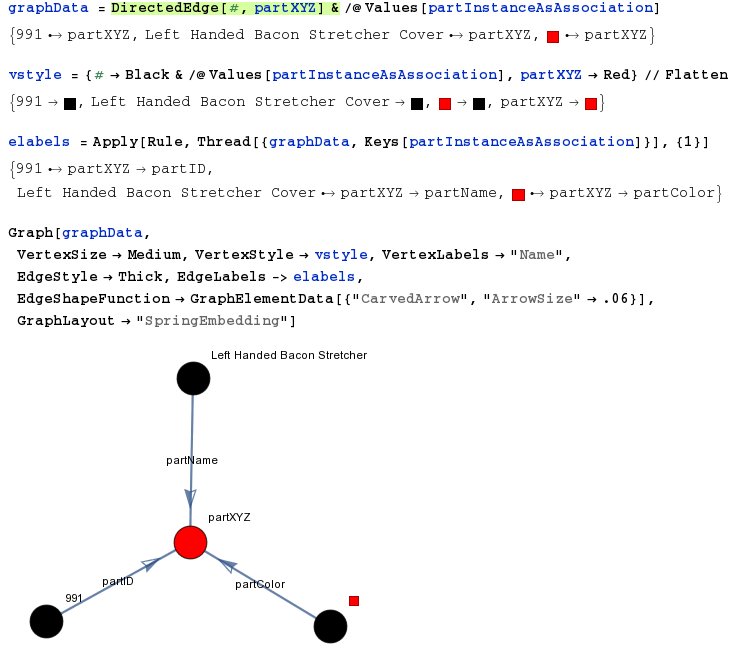
4. Tree
Wolfram Language functions are tree data structures that are created in the memory as a contiguous array of pointers, the first to the head and the rest to its successive elements. Take for example the List we defined, we can present it in a tree form with the command :
In: {991, "Left Handed Bacon Stretcher Cover", Red} // TreeForm
Similarly we can represent this row of data as a function with three arguments that take values from the Integer, String, and Color domain, e.g. :
In: partFunction[991, "Left Handed Bacon Stretcher Cover", RGBColor[1,0,0]] // TreeForm
Out: 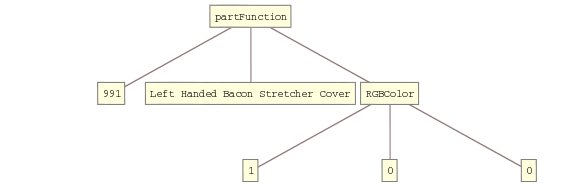
5. Association
Associations in Wolfram Language are very similar to the Association Type construct of the Topic Map data model. Each defined association is an instance of an association type. The keys of the association, association role types according to Topic Maps terminology, describe the role type of each value in the association instance. The values of the association, association role players according to Topic Maps terminology, describe the particular instance of the association type.
The command to perform the association of attributes with their values is the following
In: AssociationThread[attributes->partInstanceAsList]
Out: <|"pid"->991, "pname"->"Left Handed Bacon Stretcher Cover", "pcolor"->Red|>
In: Keys@<|"pid"->991, "pname"->"Left Handed Bacon Stretcher Cover", "pcolor"->Red|>
Out: {partID, partName, partColor}
In: Values@<|"pid"->991, "pname"->"Left Handed Bacon Stretcher Cover", "pcolor"->Red|>
Out: {991, "Left Handed Bacon Stretcher Cover", Red}
Association is a relatively new fundamental construct in Wolfram Language, it acts like a symbolically indexed list. The main reason for using it is to allow highly efficient lookup and updating and also build complex hierarchical structures and other datasets.
6. List of Rules
You can easily convert an Association to a List of Rules
In: <|"pid"->991, "pname"->"Left Handed Bacon Stretcher Cover", "pcolor"->Red|> //Normal
Out: {"pid"->991, "pname"->"Left Handed Bacon Stretcher Cover", "pcolor"->Red}
6. Hypergraph
In the following hypergraph representation we keep separate the schema from the data, i.e. the types from instances.
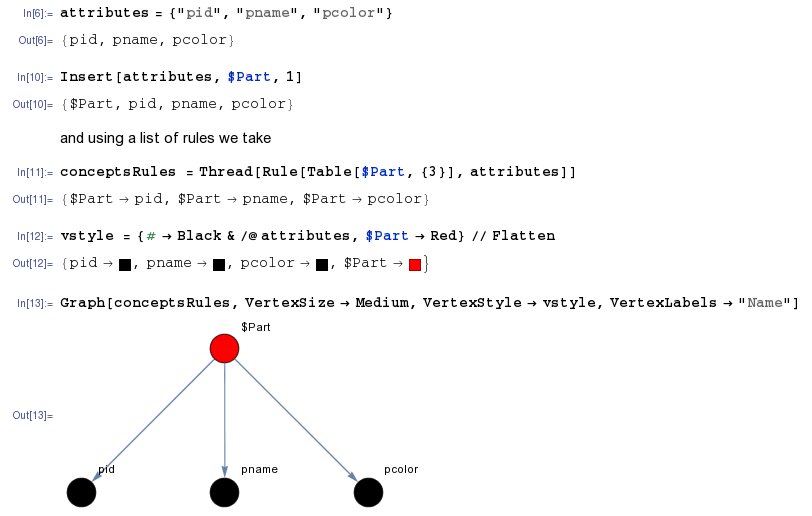
In this hypergraph the $Part plays the role of the hyperedge (red color) that connects three hypernodes that represent the attributes pid, pname, and pcolor (black color). Similarly for the values we have:
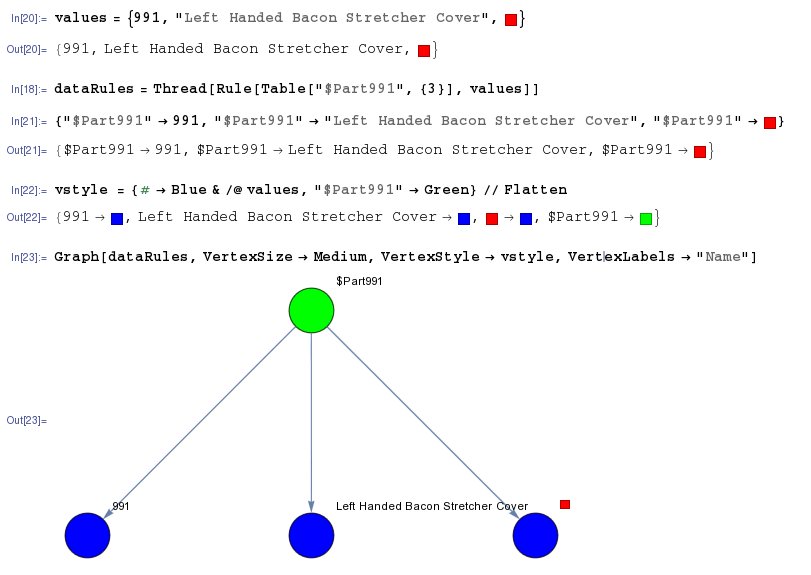
In this hypergraph the $Part991 plays the role of a hyperedge (green color) that connects three hypernodes that represent the values 991, “Left Handled….”, RED (blue color).
We defined two hyperedges, one at a layer of concepts to represent the head of the record, and another at the data layer to represent the body of the record.
7. EntityPropertyAssociation
In: Association[$Part991-> <|"partID"->991, "partName"->"Left Handed Bacon Stretcher Cover", "partColor"->Red|> ]
Out: <| $Part991 -> <|partID->991, partName->"Left Handed Bacon Stretcher Cover", partColor->Red|> |>
Table Representations
1. List of Lists
In: partsList = SQLSelect[conn, "Parts", "ShowColumnHeadings"->True]
Out: {
{"pid", "pname", "pcolor"},
{991, "Left Handed Bacon Stretcher Cover", "Red"},
{992, "Smoke Shifter End", "Black"},
{993, "Acme Widget Washer", "Red"},
{994, "Acme Widget Washer", "Silver"},
{995, "I Brake for Crop Circles Sticker", "Translucent"},
{996, "Anti-Gravity Turbine Generator", "Cyan"},
{997, "Anti-Gravity Turbine Generator", "Magenta"},
{998, "Fire Hydrant Cap", "Red"},
{999, "7 Segment Display", "Green"}
}
2. List of Associations
head = partsList[[1]];
body = partsList[[2 ;;]];
AssociationThread[head -> #] & /@ body
{
<|pid->991,pname->Left Handed Bacon Stretcher Cover,pcolor->Red|>,
<|pid->992,pname->Smoke Shifter End,pcolor->Black|>,
<|pid->993,pname->Acme Widget Washer,pcolor->Red|>,
<|pid->994,pname->Acme Widget Washer,pcolor->Silver|>,
<|pid->995,pname->I Brake for Crop Circles Sticker,pcolor->Translucent|>,
<|pid->996,pname->Anti-Gravity Turbine Generator,pcolor->Cyan|>,
<|pid->997,pname->Anti-Gravity Turbine Generator,pcolor->Magenta|>,
<|pid->998,pname->Fire Hydrant Cap,pcolor->Red|>,
<|pid->999,pname->7 Segment Display,pcolor->Green|>
}
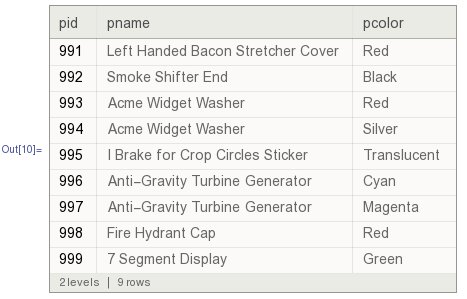
3. Dataset
head = partsList[[1]];
body = partsList[[2 ;;]];
AssociationThread[head -> #] & /@ body //Dataset
Constraints
Constraints provide one method of implementing business rules in the database. SQL implements constraint functionality in the form of check constraints. Constraints restrict the data that can be stored in relations. These are usually defined using expressions that result in a boolean value, indicating whether or not the data satisfies the constraint - Wikipedia
Constraints can apply to single attributes, to a tuple (restricting combinations of attributes) or to an entire relation. Since every attribute has an associated domain, there are constraints (domain constraints). The two principal rules for the relational model are known as entity integrity and referential integrity - Wikipedia